반응형
베르누이 분포(Bernoulli Distribution)
- 결과가 성공 아니면 실패, 두가지로 귀결되어 나오는 이산확률분포

이항분포(Binomial Distribution)
- 베르누이 시행을 n번 독립적으로 시행할 때 성공횟수를 X로 정의한 이산확률분포
- p : 성공확률
- q : 실패확률 = 1-p

- 예) 동전을 3번 던졌을 때 앞면이 나오는 횟수를 X라고 할 때 앞면이 두번 나올 확률?

- 확률은 3/8
- 기댓값은 np, 즉 3 * 1/2 = 3/2
- 분산은 npq, 즉 3 * 1/2 * 1/2 = 3/4
다항분포(Multinomial Distribution)
- 여러 개의 값을 가질 수 있는 독립 확률변수들에 대한 확률분포
- 여러 번의 독립적 시행에서 각각의 값이 특정 횟수가 나타날 확률을 정의하는 분포

- 예) 어느 공항의 항공기 이착률 상황에 대한 이상적인 조건을 알아보기 위해 컴퓨터 시뮬레이션이 수행되었을 때, 3개의 활주로가 있는 공항에서 각 활주로가 사용될 확률은 다음과 같고, 임의로 도착하는 6대의 비행기가 다음과 같이 활주로에 도착할 확률은 다음과 같다.

- 이 경우 다항 분포의 확률은?

포아송분포(Poisson Distribution)
- 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산확률분포
- 단위공간이나 면적 등에도 적용될 수 있음
- 예) 특정 시간대에 은행창구에 도착한 고객의 수, 책 한페이지당 오탈자의 수 등

- 예) 대형 호텔 자료에 따르면 통상적으로 호텔 예약자의 5%는 예약을 취소한다고 알려져 있다. 한 지역의 호텔 객실수가 95개인 한 지점에서 예약건수가 100이라고 할 때, 당일 호텔에 도착한 사람들이 모두 호텔에 들어갈 확률은?
- 예약자의 5%는 예약취소를 하니 예약건수가 95이하면 모두 투숙 가능함
- 즉 n=100, p=0.05라고 하면, 포아송근사에 의해 기댓값은 100 * 0.5
- 확률변수 X를 호텔 취소수라고하면 P(X>=5)

기하분포(Geometric Distribution)
- 베르누이 시행에서 처음 성공까지 시도한 횟수를 분포화한 이산확률분포

- 예) 어떤 학생이 한 자격증 시험에 합격할 확률은 0.7이다. 이 학생이 4번만에 붙을 확률은?
- X는 응시횟수라고 정의

음이항분포(Negative Binomial Distribution)
- x번의 베르누이 시행에서 k번째 성공할 때까지 계속 시행하는 실험에서의 확률을 나타내는 이산확률분포
- 전체 x번의 시행에서 생각해보면 x-1까지 k-1개의 성공이 있어야 함
- 이 경우 실패 갯수는 (x-1) - (k-1) = x-k
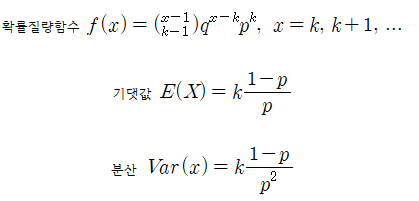
- 예) 한국시리즈는 7전 4선승제로 치루어진다. 두 팀의 승률을 안다고 할 때 각 팀이 실제 7번 경기만에 우승이 결정될 확률을 계산해보기
- A팀의 승률이 0.7, A팀이 7전째 우승할 확률은? (즉, 4승할 확률)
- k=4, p=0.7
- A팀의 승률이 0.7, A팀이 7전째 우승할 확률은? (즉, 4승할 확률)
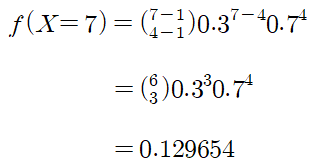
초기하분포(Hypergeometric Distribution)
- 비복원 추출에서 N개 중에 n개를 추출했을 때, 원하는 것 k개가 뽑힐 확률을 나타내는 이산확률분포

- 예) 한 공장에서 제품을 생산하는데 한 포장박스에 12개의 제품을 넣는다. 검사자는 한 박스에서 3개를 무작위로 뽑아 검사할 때 박스에 5개의 불량품이 있다고 하면 검사자가 뽑은 3개 중 불량품이 1개가 들어갈 확률은?
- 확률변수 X는 표본(n=3) 중 우리가 원하는 값은 k=1, 여기서 N=12, K=5
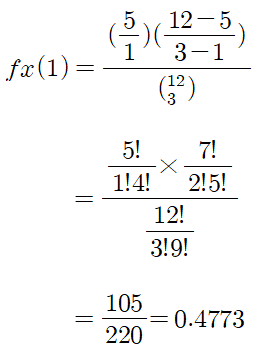
참고
반응형

