반응형
통계학의 개념
- 통계학
- 불확실한 상황에서 불확실성을 감소시키고 현명한 의사결정을 하기 위한 이론과 방법의 체계
- 수치화된 자료의 수집, 분류, 분석과 해석의 체계를 갖춘 학문
- 기술통계
- 분석에 필요한 데이터를 요약하고 묘사/설명하는 통계기법
- 추측(추론)통계
- 표본에 내포되어 있는 정보를 이용하여 모집단에 대한 과학적인 추론을 하는 통계기법
- 확률과 확률분포
- 모집단에 대한 추측 및 추론이 얼마나 정확한지에 대한 논리적 타당성을 제시하는 도구
확률의 개념
- 통계적 현상
- 고유의 법칙성을 찾아내는 것이 가능한 현상을 지칭
- 불확정 현상을 반복하여 관찰
- 집단 안에서 대량으로 관찰
- 고유의 법칙성을 찾아내는 것이 가능한 현상을 지칭
- 확률 실험
- 같은 조건 아래에서 반복 시행
- 시행의 결과는 매번 우연적으로 변하므로 예측할 수 없음
- 그러나 가능한 모든 결과의 집합을 알 수 있음
- 반복할 때 낱낱의 결과는 불규칙하게 나타남
- 반복의 수를 늘리면 어떤 규칙성이 나타나는지 특징을 가질 수 있음
확률
- 통계적 현상의 확실함의 정도를 나타내는 척도
- 랜덤 시행에서 어떠한 사건이 일어날 정도를 나타내는 사건에 할당된 수
수학적 확률(Mathematical Probability)
- 표본공간 S의 각 사건이 일어날 가능성이 동등 할 때, 사건 A에 대하여 n(A)/n(S)를 사건 A의 수학적 확률이라고 함
- n(A) : 사건 A가 일어날 경우의 수
- n(S) : 전체 사건에 대한 경우의 수
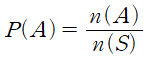
- 즉, 간단히 표현한 수식은 다음과 같음
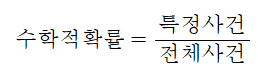
- 예) 주사위를 던질때 1이 나올 확률은 1/6
- n(A) : 1이 나올 경우의 수
- n(S) : 전체 사건(총 6의 수)에 대한 경우의 수
통계적 확률(Statistical Probability)
- 사건이 일어나는 확률을 상대도수에 의해 추정
- n회의 시행에서 문제의 사건이 r회 일어났다고 하면 상대도수는 r/n으로 정의
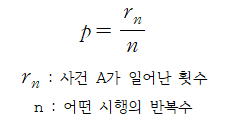
- 예) 출생한 남자 500명이 30세에 생존자 수가 440명일 경우의 살아 있을 확률은?
- 440/500 = 88%, 통계적으로 0세부터 30세까지의 생존률은 88%
사건(Event)
- 시행 : 동일한 상태로 여러 차례 반복할 수 있는 실험이나 관측
- 사건 : 시행의 결과로서 나타나는 것
- 사건은 개별적으로 발생할 결과일 수도 있고, 몇 가지의 복합된 결과의 집합일 수도 있음
- 어떤 사건의 확률은 그 사건에 포함되어 있는 각 결과의 발생 확률의 합으로 표현
- 예) 두 개의 동전을 던졌을 때, 하나만 앞면만 나올 사건의 확률은?
- [앞,뒤]가 나올 사건의 확률(1/4)
- [뒤,앞]이 나올 사건의 확률(1/4)
- 합(2/4) = 1/2
표본공간(Sample Space)
- 통계적 실험에서 모든 발생 가능한 실험결과들의 집합을 의미
- 전사건 : 표본공간 자체
- 공사건 : 아무것도 포함되지 않은 사건
- 근원사건 : 하나의 결과를 포함하는 사건
- 표본공간이 S인 확률 실험에서 사건은 S의 부분집합
- 예) 두 개의 동전을 던졌을 때, 표본공간 S의 정의
- S = { (앞,앞), (앞,뒤), (뒤,앞), (뒤,뒤) }
- 이때, 앞면이 적어도 한 번 나오는 사건 A의 정의
- A = { (앞,앞), (앞,뒤), (뒤,앞) }
확률의 기본성질
- 어떤 사건 A가 발생할 확률은 항상 0이상이다.
- 모든 사건의 확률은 0에서 1사이에 있다.
- 존재하지 않는 사건이 일어날 확률은 0이다.
- 표본공간 S 사건이 발생할 확률은 1이다.
- 모든 가능한 사건의 확률의 합은 1이다.
- 서로 배반사건인 경우(Ai ∩ Aj = ∅)는 각 사건의 발생 확률을 더한다.
- 배반사건 : 한쪽이 일어나면 다른 쪽이 일어나지 않을 때의 두 사건
- 여사건의 확률은 1에서 해당 사건의 확률을 뺀 값과 같다.
- 여사건은 발생하지 않을 사건을 말한다.
- Ai가 Aj의 부분집합이면 Ai가 발생할 확률은 Aj가 발생할 확률보다 작거나 같다.
조건부 확률
- 사건 B가 일어났다는 조건하에서 다른 사건 A가 일어날 확률
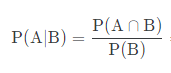
- 비슷하게 사건 A가 일어났다는 조건하에서 다른 사건 B가 일어날 확률
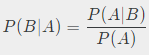
- 예) 주사위를 던져서 2의 눈이 나올 확률과 짝수라는 조건하에서의 확률
- 표본공간 : { 1,2,3,4,5,6 }
- 2의 눈이 나올 확률: { 2 }, 1/6
- 짝수가 나올 확률 : { 2,4,6 }, 1/3

결합 확률(확률의 곱셈)
- 사건 A와 B가 동시에 발생하는 확률, 이를 확률의 곱셈 법칙이라고 지칭
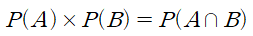

- 예) 어떤 회사가 제작하는 기계가 1년내 고장 가능성이 20%이고, 2대의 기계를 구입할 때, 1년 내에 두 기계가 모두 고장날 확률과 정확히 한 기계만 고장날 확률은?
- 모두 고장날 확률
- 두 사건은 서로 독립이므로 P(A)=0.2, P(B)=0.2
- P(A∩B) = P(A) * P(B) = 0.2 * 0.2 = 0.04
- 모두 고장날 확률 4%
- 정확히 한 기계만 고장날 확률
- P(A여사건 ∩ B) + P(A ∩ B여사건)
- = P(A여사건) * P(B) + P(A) * P(B여사건)
- = 0.8 * 0.2 + 0.2 * 0.8 = 0.32
- 정확히 한 기계만 고장날 확률 32%
- 모두 고장날 확률
총확률정리(Total Probability Rule)
- 임의의 사건 B의 확률을 k개의 조건부 확률을 이용해서 구하는 것
- 임의의 사건 P(B)는 다음과 같이 표현 가능

베이지안 정리(베이즈 정리, Baye's Theorem)
- 총확률정리를 이용하여 임의의 사건 B의 확률을 k개의 조건부 확률을 이용해 계산
- 베이지안 법칙을 이용하여 표본공간을 분할하는 k개의 상호 배타적인 사건 Ai에 대한 사후확률을 구할 수 있음
- 사전 확률 : P(Ai), 미리 주어진 사건 A가 발생할 확률
- 사후 확률 : 사건 B라는 새로운 사건 발생시 P(Ai | B)의 확률
- 사전에 어떤 사건 A에 대한 사전확률이 부여된 상태에서 어떤 사건 B에 관한 정보가 알려진 후, 그 사건 A에 대한 사후확률은 다음과 같이 정리 가능

- 예) 직장 남성의 30%는 지나친 흡연으로 기관지 이상이 있다고 알려져 있다. 실제 기관지 검사를 했을 때, 검사 결과 90%가 이상이 있고, 기관지에 이상이 없는 경우에도 이상반응이 나타날 수 있는 확률이 10%, 임의의 직장 남성이 기관지 검사를 하였을 때 이상반응이 나타났지만 실제로 이상이 없을 확률은?
- P(A1) = 0.3, P(A2) = 0.7
- A1 : 기관지에 이상이 있을 사건, 30%
- A2 : 기관지에 이상이 없을 사건, 70%
- P(B|A1) = 0.9, P(B|A2) = 0.1
- B : 검사결과 이상반응이 나타날 사건, 10%
- 0.9 * 0.3 + 0.1 * 0.7 = 0.34
- 0.9 * 0.3 : 기관지 이상이 있고, 검사 결과 이상이 있는 경우
- 0.1 * 0.7 : 기관지 이상이 없고, 검사 결과 이상이 있는 경우
- 임의의 직장 남성이 기관지 검사를 하였을 때 이상을 보일 확률 34%
- 0.07 / 0.34 = 0.2058..., 20.56%
- 검사결과 이상이 있는것으로 나타난 사람에게 실제로 기관지에 이상이 없을 사후 확률은 20.6%
- P(A1) = 0.3, P(A2) = 0.7
참고
반응형

