반응형
확률변수(Random Variable)
확률변수의 개념
- 사건의 시행의 결과(확률)를 하나의 수치로 대응시킬 때의 값(확률)
- 일반적으로 대문자 X로 표기
- 예) 동전 두 개를 던져 앞면이 나오는 횟수를 확률변수 X라고 가정
- 4가지의 경우 발생 { (뒤,뒤), (앞,뒤), (뒤,앞), (앞,앞) }
- 확률변수 X의 값
- X(뒤,뒤) = 0
- X(앞,뒤) = 1
- X(뒤,앞) = 1
- X(앞,앞) = 2
- { 0,1,2 } 총 3가지
- 확률변수 X가 특정한 값 x를 가질 때 그에 대한 확률 P(X=x)로 표기
- 앞면이 2개 나올 확률 P(X=2)
확률변수의 종류
- 이산확률변수(Discrete Random Variable)
- 확률변수가 취할 수 있는 값의 수가 유한한 변수
- 확률변수 X가 X={0,1,2,3} 같이 셀 수 있는 값을 의미
- 연속확률변수(Continuous Random Variable)
- 확률변수가 취할 수 있는 값의 수가 무한한 변수
- 확률변수 X가 키, 몸무게, 시간 같이 셀 수 없는 연속적인 값을 의미
- 확률변수가 특정한 값을 취 할 때의 확률이 아닌 특정 구간 내에서의 확률 값을 구함
- P(a<=X<=b) 로 표기
- 예) 확률변수 X가 어떤 집단의 몸무게를 나타낼 때 몸무게가 50에서 60일 확률 P(50<=X<=60)
확률분포
확률분포의 개념
- 수치로 대응된 확률변수의 개별 값들이 가지는 확률값의 분포
- 예) 두 개의 주사위를 던져서 나오는 점들의 합
| y | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| P(Y=y) | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
- 확률변수가 취할 수 있는 구체적인 값을 확률공간상의 확률값으로 할당
이산확률분포(Discrete Probability Distribution)
- 확률변수가 취할 수 있는 값의 수가 유한한 확률분포
확률질량함수(Probability Mass Function)
- 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수 f(x)=P(X=x)
- = 불연속한 값에 대한 확률을 나타내는 함수
- 0과 1 사이의 값을 가짐
- 음수를 함숫값으로 가질 수 없음
- 함숫값을 모두 더하면 1
- 예) 주사위를 한 번 던질 때의 값을 나타낸 확률 변수 X의 확률질량함수
- f(x)= 1/6
연속확률분포(Continuous Probability Distribution)
- 확률변수가 취할 수 있는 값의 수가 무한한 확률분포
확률밀도함수(Probability Density Function)
- 확률 변수의 분포를 나타낸 함수



확률분포함수(Probability Distribution Function, 확률함수)
- 확률변수가 취할 수 있는 구체적인 값 하나하나를 확률 공간상의 확률값으로 할당해주는 함수
- 이산확률분포함수 : 확률변수가 이산적인 확률분포를 가지는 함수
- 연속확률분포함수 : 확률변수가 연속적인 확률분포를 가지는 함수
확률변수의 기댓값과 분산
기댓값(Expected Value)
- 각 확률변수가 특정 값을 가질 확률을 가중치로 확률변수의 결과값을 평균화한 값으로 표시
- 즉, 어떤 확률 과정을 무한히 반복했을 때 얻을 수 있는 값들의 평균으로 기대하는 값
이산확률변수의 기댓값

- 예) 주사위를 한 번 던졌을 때, 기댓값은?
- 각 눈의 값이 나올 확률은 1/6
- 주사위 값의 기댓값은 각 눈의 값에 그 확률을 곱한 값의 합으로 구함

연속확률변수의 기댓값
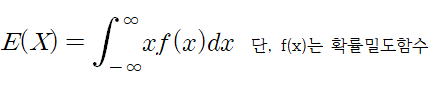
- 예) 구간[0,1]에서 연속인 확률변수 X의 확률밀도함수 f(x)=1이라고 하면, X의 기댓값은?

기댓값의 성질
기댓값의 선형성
- 상수 a, b와 확률변수 X에 대해서 다음 식이 성립함

기댓값의 덧셈법칙
- 두 확률변수 X, Y에 대하여 X+Y의 기댓값은 X의 기댓값과 Y의 기댓값을 더한 것과 같음
- 두 확률변수가 독립이든, 종속이든 무관하게 항상 성립함

기댓값의 곱셈법칙
- 두 확률변수 X, Y에 대하여 일반적으로 곱셈법칙이 성립하지 않음
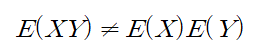
- 하지만, 두 확률변수 X, Y가 독립이면 곱셈법칙이 성립함
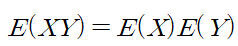
분산(Variance)
- 확률분포의 산포도(퍼짐정도)를 나타내는 측도
- 분산은 음의 값을 가질 수 없음
- 분산이 클수록 확률분포는 평균에서 멀리 퍼져 있음
- 0에 가까워질수록 평균에 집중
- 기댓값에서 떨어진 거리의 제곱의 기댓값(평균)이며 Var(X)로 표시
이산확률변수의 분산

연속확률변수의 분산
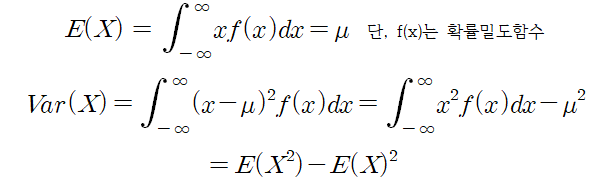
분산의 성질
- 상수 a를 확률변수에 곱했을 때 분산은 a의 제곱
- 상수 b를 확률변수에 더했을 때 기대값에 영향 없음
- 확률변수 X와 Y가서로 독립이면 각각의 분산의 합은 같음
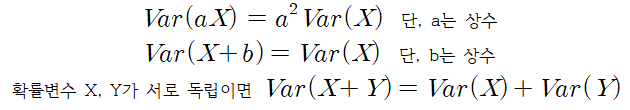
참고
반응형

