딥러닝 - 심층신경망(Deep Neural Network, DNN)

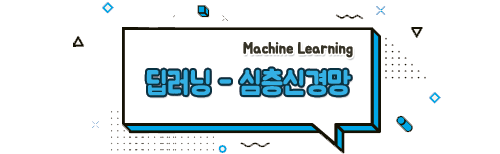
심층 신경망(Deep Neural Network, DNN)

• 입력층(input layer)과 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)들로 이루어진 인공 신경망
• 일반적인 인공 신경망과 마찬가지로 복잡한 비선형 관계들을 모델링 할 수 있음
  • 예: 물체 식별 모델을 위한 심층 신경망 구조에서는 각 물체가 영상의 기본적인 요소들로 계층적 구성 표현
• 비슷한 기능을 하는 인공 신경망에 비해 더 적은 수의 유닛(노드)들 만으로도 복잡한 데이터를 모델링 할 수 있음

---

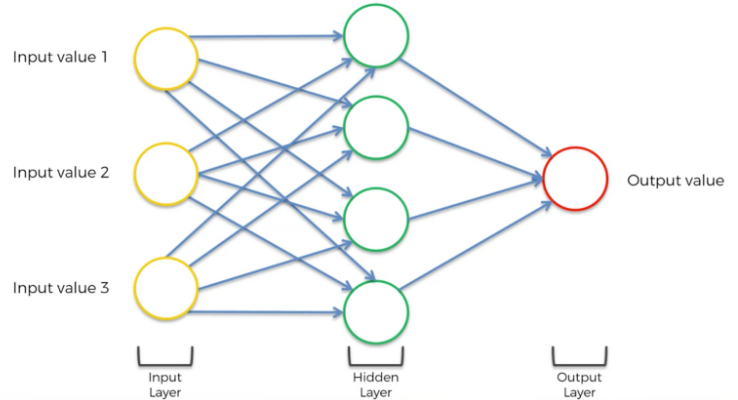
심층 신경망 알고리즘

• 순전파와 역전파를 이용하여 오차 최소화
  • 순전파 (feedforward) : 입력층에서 출력층으로 데이터를 전달
  • 역전파(backpropagation) : 출력층에서 입력층으로 데이터를 반대로 전달

 

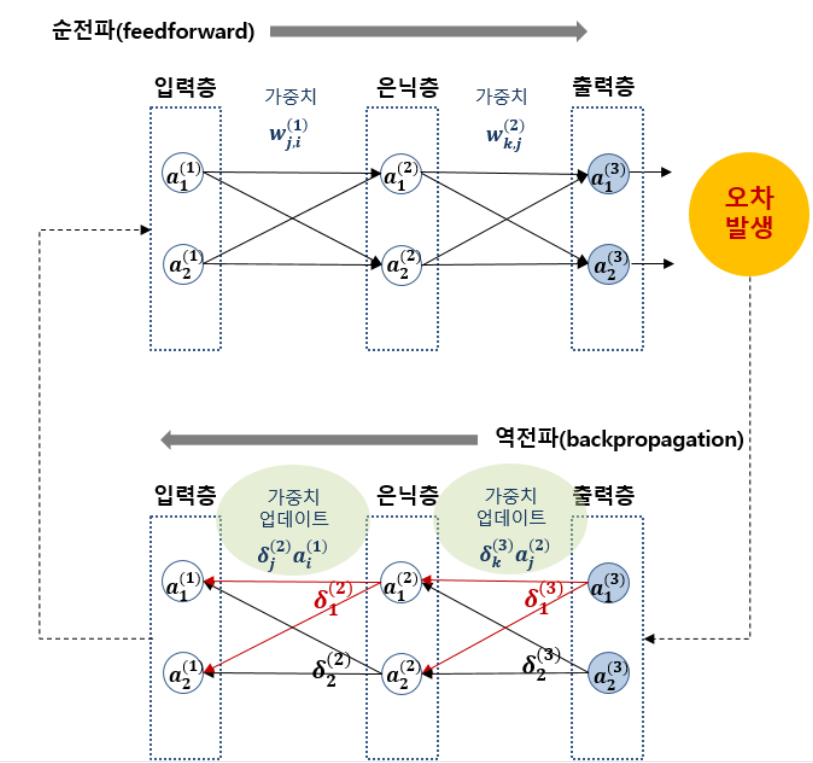
• 오차역전파법과 경사 하강법은 구현의 용이함과 국지적 최적화(local optima)에 잘 도달한다는 특성으로 인해 다른 방법들에 비해 선호
  • 오차역전파법 (backpropagation)
    • 출력층에서 제시한 값이 실제 원하는 값에 가까워지도록 학습하기 위해 사용하는 통계적 기법 
    • 동일 입력층에 대해 원하는 값이 출력되도록 개개의 가중치를 조정하는 방법으로 사용
    • 출력층에서 입력층까지 오차를 전달하여 가중치를 수정해나가는 알고리즘
      • 오차를 구하여 오차가 최소가 될 때까지 가중치의 값을 변경
        • 오차 : 데이터에 존재하는 목표 값 - 심층 신경망이 계산한 값
  • 경사 하강법 (gradient descent)
    • 1차 근삿값 발견용 최적화 알고리즘
    • 함수의 기울기를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를때까지 반복
      • 오차/손실 함수(error/loss function)를 이용하여 기울기의 크기를 줄임
      • 오차/손실 함수는 제곱 오차(squared error)를 이용
        • 제곱 오차 : (데이터가 존재하는 목표 값 - 심층 신경망이 계산한 값)²
  • 심층 신경망은 오차역전파 알고리즘으로 학습, 가중치들은 확률적 경사 하강법을 통하여 갱신

---

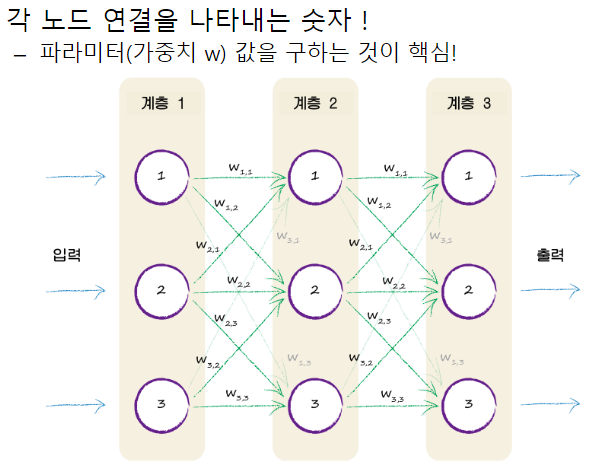
심층 신경망의 문제점

• 추가된 계층들이 학습 데이터의 낮은 의존성을 가지는 모형화가 가능하도록 해주기 때문에 과적합과 높은 시간 복잡도가 흔히 발생
• 학습 시킬 때 시간 복잡도가 매우 높으므로 크기(계층의 수와 계층 당 유닛(노드) 수), 학습률, 초기 가중치(weight) 등 많은 매개변수(parameter) 고려