반응형
베이즈 추론
- 베이즈(베이지안) 확률론을 기반으로 통계적 추론의 한 방법
- 추론 대상의 사전 확률과 추가적인 정보를 통해 해당 대상의 사후 확률을 추론하는 방법
- 추론하는 대상을 확률변수로 보아 그 변수의 확률분포를 추정하는 것
확률론적 의미해석(조건부 확률)

베이즈 기법의 개념
- 객관적 관점
- 베이즈 통계의 법칙은 이성적, 보편적으로 증명될 수 있으며 논리의 확장으로 설명될 수 있음
- 주관주의 확률 이론의 관점
- 지식의 상태는 개인적인 믿음의 정도(Degree of Belief)로 측정
- 확률에 대한 여러 개념 중 가장 인기있는 것 중 하나로 심리학, 사회학, 경제학 이론에 많이 응용
- 어떤 가설의 확률을 평가하기 위해 사전 확률을 먼저 밝히고 새로운 관련 데이터에 의한 새로운 확률값 변경
베이즈 기법 적용
회귀분석모델에서 베이즈 기법의 적용
- 선형회귀분석모델(Linear Regression)
- 추정치와 실제의 차이(loss)를 최소화하는 것
- 기존 머신러닝의 방법
- 경사하강법과 같은 알고리즘을 통해 점진적으로 학습하여 매개변수 확인
- 경사하강법 : 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복
- 베인지안 확률론의 적용개념
- P(Model)이라는 사전 확률(prior)을 알고 있음
- 새로운 데이터가 관측되면 P(Model|Data)이라는 사후 확률(posterior)을 얻음
- 다음 번 학습의 사전확률로 사용
- 즉, 점진적으로 P(Model), 즉 매개변수(parameter)들의 분포를 찾아가는 과정
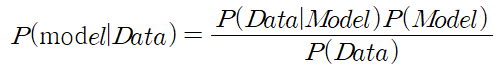
분류에서 베이즈 기법의 적용
- 나이브 베이즈 분류(Naive bayes Classification)
- 특성들 사이의 독립을 가정하는 베이즈 정리를 적용한 확률 분류기를 지칭
- 나이브 베이즈의 특성
- 분류기를 만들 수 있는 간단한 기술
- 단일 알고리즘을 통한 훈련이 아닌 일반적인 원칙에 근거한 여러 알고리즘들을 이용하여 훈련
- 모든 나이브 베이즈 분류기는 공통적으로 모든 특성 값이 서로 독립임을 가정
- 예) 특정과일을 귤로 인식(분류)하게 하는 특성을 생각해보면?
- 노란색, 둥글다, 표면이 울퉁불퉁, 지름이 5cm인 특성
- 나이브 베이즈 분류기에서는 아무런 연관성이 없음. 즉, 독립사건임
- 나이브 베이즈의 장점
- 일부 확률모델에서 나이브 베이즈 분류는 지도학습 환경에서 매우 효율적으로 훈련
- 분류에 필요한 파라미터를 추정하기 위한 트레이닝 데이터의 양이 매우 적음
- 간단한 디자인과 단순한 가정에도 불구하고 많은 복잡한 실제 상황에서 잘 작동
- 나이브 베이즈 분류기의 생성(확률모델)
- 나이브 베이즈는 조건부 확률 모델
- 분류될 인스턴스들은 N개의 특성(독립변수)을 나타내는 벡터(X = x1, x2, ..., xn)로 표현
- 벡터를 이용하여 k개의 가능한 확률적 결과들(클래스)을 할당
- 아래의 식을 이용하지만 결국 표현만 다를 뿐 식은 같음
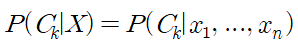
- 이벤트 모델
- 특성의 분포에 대한 여러 가정들을 나이브 베이즈 분류 이벤트 모델이라고 지칭
- 클래스의 사전확률은 클래스간 동일확률을 가정하여 계산 가능
- 사전확률 = 1 / 클래스의 수
- 트레이닝 셋으로부터 클래스의 확률의 추정치 계산 가능
- 해당 클래스의 사전확률 = 해당 클래스의 샘플 수 / 샘플의 총 수
- 특성의 분포에 대한 모수 추정
- 트레이닝 셋의 특성을 위한 비모수 모델이나 분포를 가정 또는 생성
- 이벤트 모델의 종류
- 가우시안 나이브 베이즈
- 연속적인 값을 지닌 데이터를 처리 할 때 사용
- 각 클래스의 연속적인 값 벡터(X = x1, x2, ..., xn)들이 가운시안 분포를 따른다고 가정
- 다항분포 나이브 베이즈
- 특성 벡터(X = x1, x2, ..., xn)들이 다항분포에 의해 생성된 이벤트의 경우 사용
- 베르누이 나이브 베이즈
- 특성 벡터(X = x1, x2, ..., xn)들이 독렙된 이진 변수로 표현될 경우 사용 (예: 성공/실패)
- 가우시안 나이브 베이즈
- 나이브 베이즈 분류의 적용
- 분류기반의 머신러닝 적용을 하는데 광범위하게 사용
- 예시) 문서분류(스팸분류) 등
참고
반응형

