반응형
시계열분석의 정의
- 시계열 자료(data)를 분석하고 여러 변수들 간의 인과관계를 분석하는 방법론
- 경제학에서도 매우 많이 쓰이는 방법론을ㄹ 계량경제학이나 금융, 거시경제 분석에 사용
- 시계열자료의 구분, 정상성 구분에 따른 분석 모델 그리고 회귀분석에 대해서 이해할 수 있어야 함
시계열 자료
- 시간의 흐름에 따라서 관측되는 데이터
- 미래에 대해 예측 또는 제어하는 것이 주 이용 목적
- 이산 시계열 : 관측값들이 이산적인 형태로 분리되어 존재
- 연속 시계열 : 관측값들이 연속적으로 연결된 형태의 자료
- 시차(Time lag) : 한 관측시점과 다른 관측시점 사이의 간격
시계열 자료 성분
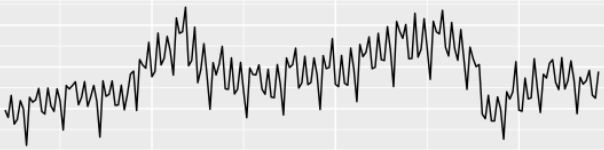
불규칙 성분(Irregular Component)
- 시간에 따른 규칙적인 움직임이 없는(무관하게) 랜덤하게 변화하는 변동성분
- 시계열 자료가 추세 성분, 계절 성분, 순환(주기) 성분을 제외하고 나머지 불규칙한 변동을 보이는 경우를 의미
체계적 성분(Systemic Component)
- 시간에 다른 규칙이 존재하는 변동성분
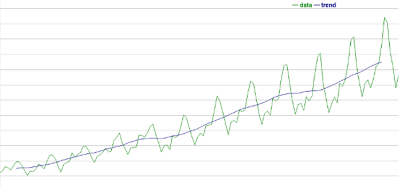
추세 성분(Trend Component)
- 관측 값이 지속적으로 증가 또는 감소하는 추세(Trend) 포함

계절 성분(Seasonal Component)
- 주기적 성분에 의한 변동을 가지는 형태(계절, 주, 월, 년 등)

순환 성분(Cyclical Component, 주기 성분)
- 주기적 변화를 가지나 계절적인 것이 아닌 주기가 긴 변동을 가지는 형태(경기 대순환, Business Cycle)
- 계절 성분과 같이 일정한 주기로 반복되지만 그 주기가 정확히 알려져 있지 않거나 변할 수 있는 경우를 의미
복합 성분
- 추세 성분과 계정 성분을 동시에 가지는 경우를 의미
자기상관성(Autocorrelation)
- 시계열 자료에서 시차값들 사이에 선형관계를 보이는 것
백색잡음(White Noise)
- 자기 상관성이 없는 시계열 데이터
- 아무런 패턴이 남아있지 않은 무작위한 움직임(진동)을 보이는 데이터
정상성(Stationarity)
- 시계열 자료가 평균과 분산이 일정한 경우
- 일반적으로 시계열 자료가 정상성을 가지면 분석이 용이한 형태를 가짐
- 평균이 일정한 경우
- 모든 시점에 대해 평균이 일정함
- 시계열 자료가 평균이 일정하지 않으면 차분(differenece)을 통해 정상성을 가지도록 함
- 분산이 일정한 경우
- 모든 시점에서 분산이 일정함
- 시계열 자료가 분산이 일정하지 않으면 변환(transformation)을 통해 정상성을 가지도록 함
- 공분산의 경우도 단지 시차에만 의존하며 특정시점에는 의존하지 않음
- 정상성을 가지는 시계열 자료의 특징
- 정상시계열은 어떤 시점에서 평균분산 그리고 특정시차가 일정한 경우의 공분산 동일
- 항상 평균회귀 경향이 있으며 평균 주변의 변동은 대체로 일정한 폭을 가짐
- 특정기간에서 얻은 정보를 다른 시기에서도 사용이 가능한 정보로 일반화 가능
- 반대로 정상성을 가지지 않는 경우는 일반화하기 어려움
시계열자료의 분석 방법
| 예측 목적 중심의 분석 방법 개요 | ||
| 예측 목적 (Forecast) |
단순 방법 |
- 추세분석(Trend Analysis) 평균 - 평활법(Smoothing Method) - 분해법(Decomposition Method) |
| 모델 기반 |
- 자기회귀모델 (AR, AutoRegressive Model) - 자기회귀이동평균모델 (ARMA, AutoRegressive Moving Average Model) - 자기회귀누적이동평균모형 (ARIMA, AutoRegressive Intergrated Moving Average Model) |
|
| 이해와 제어의 목적 | - 스펙트럼분석(Spectral Analysis) - 개입분석(Intervention Analysis) |
|
단순방법
- 이동평균법(Moving Average Method)
- 과거로부터 현재까지 시계열 자료 대상
- 일정기간(관측기간)을 시계열을 이동하면서 평균을 계산하는 방법
- 추세를 파악하여 시계열의 다음기간을 예측하는데 사용
- 데이터가 많고 안정된 패턴을 보이는 경우 추세의 판단 효용성 높음
- 지수평활법(Exponential Smoothing Method)
- 이동평균법과 달리 관찰기간의 제한이 없이 모든 시계열 데이터 사용
- 최근 시계열에 더 많은 가중치를 주며 추세를 찾는 방법
- 시간의 지수배로 가중치가 높아짐
- 과거 데이터일수록 가중치(지수적 감소)를 적게 배당
- 단기간 발생하는 불규칙 변동을 평활하는데 사용
- 중기 이상의 예측에 사용
- 단순지수평활법의 경우 장기 추세나 계절성이 포함된 시계열 자료에는 부적합
- 지수평활계수가 작으면 지엽적 변화에 민감, 크면 둔감해지는 효과
- 분해법(Decomposition Method)
- 시계열자료의 성분 분류대로 시계열 데이터를 분해하는 방법
- 시계열이 체계적 성분과 불규칙적 성분으로 이루어져 있다는 가정하에 체계적 성분을 시계열로부터 분리하여 분석/예측을 목적으로 하는 기법
- 시계열자료를 분해된 성분별로 해석하는 것이 목적
- 계절적 특성, 추세/순환 성분을 분리하여 시계열의 장기적 추이 분석
- 불규칙 성분으로부터 불규칙성이 발생한 시점 확인
- 계절조정(Seasonal Adjustment) 자료 제공, 이를 계절조정된 시계열자료라 지칭
- 체계적 성분 중 계절 성분은 종종 시계열의 장기적 변화를 살피는데 방해가 되기 때문
- 많은 공공기관에서 시계열 자료는 원자료에서 계절 성분을 뺀 자료 제공
- 즉, 원자료로부터 계절 성분을 분리한 것
모델에 의한 방법
- 자기회귀모형(AR, AutoRegressive Model)
- 현재 시점의 자료가 이전 P시점의 자료의 가중합으로 표현된다는 가정하에 만들어진 모델
- 이 때, 가중치 계수를 적절히 추정하여 모델 생성
- 즉, P시점 전의 자료가 현재자료에 영향을 준다는 가정하에 만들어진 시계열 예측 모델
- 과거의 패턴이 지속된다면 시계열 자료 관측치는 과거 관측치에 의해 예측 가능
- 어느 정도의 멀리 있는 과거 관측치까지 이용할 것인지에 대한 판단 중요
- 현재 시점의 자료가 이전 P시점의 자료의 가중합으로 표현된다는 가정하에 만들어진 모델
- 자기회귀이동평균모형(ARMA, AutoRegressive Moving Average Model)
- 자기회귀모형 + 이동평균모형 = 자기회귀이동평균모형
- 현재 시점 자료가 이전 P시점의 백색잡음의 가중합으로 표현
- 즉, 오차항에 의해서만 시계열 결정
- 자기회귀누적이동평균모형(ARIMA, AutoRegressive Integrated Moving Average Model)
- 비정상성을 가지는 시계열 자료 분석에 사용
- ARIMA(p,d,q) 형태로 정의
- 시계열 자료 X를 차분에 의해 분해해서 만들어진 시계열 자료 Y가 ARMA(p,q) 모델이면 X는 차수가 p,d,q인 ARIMA 모델
- d=0 : 자기회귀이동평균MA(p,q))이므로 정상성을 가지는 데이터가 됨
- p=0 : 누적이동평균(IMA(d,q))이므로 d번 차분하면 이동평균(MA(q)) 모델을 따름
- q=0 : 자기회귀누적(ARI(p,d))이므로 d번 차분하면 자기회귀(AR(p)) 모델을 따름
참고
- 2023 이기적 빅데이터 분석기사 필기 도서
- otexts.com - Time series decomposition
- encora.com - A Visual Guide to Time Series Decomposition Analysis
반응형

