반응형
통계적 시각화 도구
도수분포표(Frequency Table)
- 수집된 자료를 적절한 계급에 의해 분류하여 정리한 표
- 질적 자료의 경우, 각 자료값(범주)에 대하여 도수나 상대도수로 표현
- 도수(Frequency) : 질적 자료의 경우 각 범주별 빈도
- 상대도수(Relative Frequency) : 도수/전체 자료 수
- 양적 자료의 경우, 전체 자료를 그룹화(계급구간)하고 각 그룹별 속하는 자료의 수를 계산하여 도수 및 상대도수로 표현
- 예) 서울지역 초등학생 100명 대상의 빙과류 선호도 조사 도수분포표
| 상품 | 도수 | 상대도수 |
| 콘 형태 아이스크림 | 65 | 65/100=0.65 |
| 막대 형태 아이스크림 | 25 | 25/100=0.25 |
| 기타 | 10 | 10/100=0.1 |
| 합계 | 100 | 1.0 |

히스토그램(Histogram)
- 도수분포표를 이용하여 표본의 자료분포를 나타낸 그래프
막대 그래프(Bar Chart)
- 각 자료값에 대한 도수 또는 상대 도수를 그림으로 표현한 것
- 예) 서울지역 초등학생 100명 대상의 빙과류 선호도 조사 막대 그래프

파이 차트(Pie Chart)
- 각 자료값의 상대도수로 기입하여 원의 면적에 각 상대 크기별로 나타낸 그래프
- 예) 서울지역 초등학생 100명 대상의 빙과류 선호도 조사 파이 차트

산점도(Scatter Plot)
- 직교 좌표계를 이용해 두 개 변수 간의 관계를 나타내는 방법
- 이상치를 확인하는 경우에 유용하게 사용
- 범주형 데이터는 산점도로 나타낼 수 없음
- 범주형 데이터의 산점도 표시 예시) 서울지역 초등학생 100명 대상의 빙과류 선호도와 가격의 산점도


줄기 잎 그림(Stem-and-Leaf Diagram)
- 통계적 자료를 형태와 그래프 형태의 혼합된 방법으로 나타내는 것
- 자료의 정리가 가능할 뿐 아니라 자료의 구조에 대한 정보도 파악 가능한 도구
- 줄기 잎 그림 작성 절차
- 원 자료를 크기 순으로 정리
- 원 자료의 숫자를 두 부분으로 나누어 앞부분은 줄기, 뒷부분은 잎으로 함
- 줄기에 해당하는 숫자를 크기 순으로 나열
- 원 자료의 수치를 해당 줄기 우측 뒷부분에 기록
- 한 줄기에 기록된 잎의 수가 너무 많은 경우에는 두 줄로 나누어 잎을 기록할 수 있음
- 줄기 잎 그림 예시) 156, 158, 165, 167cm의 키를 줄기 잎 그림으로 표시
- 백자리와 십의자리는 줄기, 일의자리는 잎
| 줄기 | 잎 |
| 15 | 6, 8 |
| 16 | 5, 7 |
상자 수염 그림(Box Plot)
- 수치적 자료를 표현하는 그래프
- 자료로부터 얻어 낸 통계량인 5가지 요약 수치 이용하여 표현
- 5가지 요약 수치(다섯 숫자 요약, Five-number Summary)
- 최솟값, 제1사분위(Q1), 제2사분위(Q2), 제3사분위(Q3), 제4사분위(Q4), 최댓값을 일컫는 말
- 상자 수염 그림 작성 절차
- 주어진 데이터에서 각 사분위수 계산
- 그래프에서 제1사분위와 제3사분위를 밑변으로 하는 직사각형을 그리고, 제2사분위에 해당하는 위치에 선분을 그음
- 사분위범위(IQR: Interquartile Range, Q3-Q1) 계산
- Q3과 차이가 1.5IQR 이내인 값중에서 최댓값을 Q3과 직선으로 연결하고, 마찬가지로 Q1과 차이가 1.5IQR 이내인 값 중에서 최솟값을 Q1과 연결
- Q3보다 1.5IQR 이상 초과하는 값과 Q1보다 1.5IQR 이상 미달하는 값은 점이나 원, 별표 등으로 따로 표시(이상치 점)
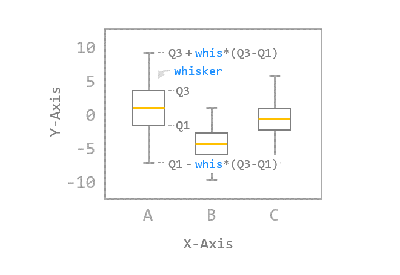
참고
반응형

