반응형
변수 간의 상관성 분석
- 두 변수 간 어떤 선형적 관계를 갖고 있는지 분석하는 방법
* 상관관계(correlation) : 두 변수는 서로 독립적인 관계이거나 상관된 관계 일 수 있으며, 이 때 두 변수 간 관계의 강도를 나타낸 것을 의미
- 단순상관분석(Simple Correlation Analysis)
- 단순히 두 개의 변수가 어느 정도 강한 관계에 있는가 측정
- 다중상관분석(Multiple Correlation Analysis)
- 3개 이상의 변수 간의 관계강도 측정
- 편상관관계분석(Partial Correlation Analysis)
- 다중상관분석에서 다른 변수와의 관계를 고정하고 두 변수의 관계강도를 측정
상관분석의 기본가정
- 선형성
- 두 변인 X와 Y의 관계가 직선적인지 알아보는 것
- 분포를 나타내는 산점도를 통하여 확인
- 산점도란, 직교 좌표계를 이용해 두 개 변수간의 관계를 나타내는 방법
- 동변량성(등분산성, Homoscedasticity)
- X의 값에 관계없이 Y의 흩어진 정도가 같은 것
- 반의어 이분산성(Heteroscedasticity)
- 산포도가 특정 구간에 상관없이 퍼진 정도가 일정할 때를 동변량성을 띤다고 말함
- 반대로 그 정도가 일정하지 않으면 이분산성을 띤다고 말함
- X의 값에 관계없이 Y의 흩어진 정도가 같은 것
- 두 변인의 정규분포성
- 두 변인의 측정치 분포가 모집단에서 모두 정규분포를 이루는 것
- 무선독립표본
- 모집단에서 표본을 뽑을 때 표본대상이 확률적으로 선정된다는 것
상관분석 방법
피어슨 상관계수(Pearson Correlation Coefficient 또는 Pearson's r)
- 두 변수 X와 Y 간의 선형 상관관계를 계량화한 수치
- 피어슨 상관계수는 +1과 -1 사이의 값을 가짐
- +1은 완벽한 양의 선형 상관관계
- 0은 선형 상관관계 없음
- -1은 완벽한 음의 선형 상관관계
- 양의 상관관계 : 변수 X가 증가할수록 변수 Y도 증가할 때, 두 변수 사이에는 양의 상관관계가 있음

- 음의 상관관계 : 변수 X가 증가할수록 변수 Y는 감소할 때, 두 변수 사이에는 음의 상관관계가 있음

- 상관관계 없음 : 두 변수 사이에 특별한 관계가 없을 때, 두 변수는 아무 연관성이 없음

- 상관계수 예시

스피어만 상관계수(Spearman Correlation Coefficient)
- 데이터의 값 대신 순위를 이용한 상관계수
- 데이터를 작은 것부터 차례로 순위를 매겨 서열 순서로 바꾼 뒤 순위를 이용해 상관계수를 구함
- 두 변수 간의 연관 관계가 있는지 없는지를 밝혀주며 자료에 이상점이 있거나 표본 크기가 작을 때 유용
- 스피어만 상관계수는 값이 클수록 상관계수의 값도 커짐
- 한 변수의 값이 커지면 다른 변수의 값도 단조적으로 커지는지 확인
- 1에 가까울수록 두 변수는 단조적 상관성(커지면 같이 증가)을 가짐
- 0에 가까울수록 상관성이 없는 것으로 판단
- 선형관계와 단조관계

- 단조관계

- 관계 없음

피어슨 및 스피어만 상관계수 비교
- 한 변수가 증가하면 다른 변수가 일정한 양만큼 증가
- 즉, 완전한 선을 형성하는 경우
- 피어슨 및 스피어만 상관계수는 모두 +1

- 한 변수가 증가하면 다른 변수가 증가하지만 양이 일정하지 않은 관계인 경우
- 피어슨 상관계수는 양수이지만 +1보다 작음
- 스피어만 상관계수는 +1

- 관계가 랜덤이거나 존재하지 않은 경우
- 두 상관 계수 모두 0에 가까움

- 한 변수가 감소하면 다른 변수가 일정한 양만큼 감소
- 즉, 완전한 선을 형성하는 경우
- 피어슨 및 스피어만 상관계수는 모두 -1

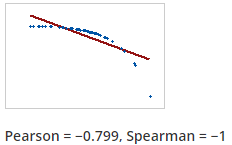
- 한변수가 감소하면 다른 변수가 증가하지만 양이 일정하지 않은 관계인 경우
- 피어슨 상관계수는 음수이지만 -1보다 큼
- 스피어만 상관계수는 -1
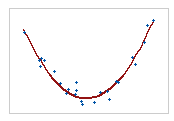
- 비선형 관계인 경우
- 피어슨 상관계수는 선형 관계만 측정, 거의 0에 가까움
- 스피어만 상관계수는 단순 관계만 측정, 거의 0에 가까움
참고
- 2023 이기적 빅데이터 분석기사 필기 도서
- 위키백과 - 상관 분석
- 위키백과 - 스피어먼 상관 계수
- KhanAcademy - 산점도와 상관관계 복습
- Minitab - Pearson 및 Spearman 상관 방법의 비교
반응형

