반응형
변수 변환의 개념
- 데이터를 분석하기 좋은 형태로 바꾸는 작업
- 어떤 변수를 나타낸 식을 다른 변수로 바꿔 나타내는 기법
- 데이터의 전처리 과정 중 하나로 간주
- 해석이 용이해지거나 취급이 단순해지는 장점 존재
변수 변환의 방법
범주형 변환
- 연속형 변수 중, 분석결과의 명료성 및 정확성을 배가시키기 위해 범주형으로 바꾸는 것
- 예) 연속형 변수 : '소득이 100만원 늘 때마다 사교육비의 지출이 10만원 증가'
- 범주형 변환 : '상위 10% 소득가정의 사교육비 지출이 하위 10%보다 10배 많다'
- 연속형 데이터를 순위형(rank) 데이터로 범주를 나누어 상대비교를 하는 방법
- 즉, 연속형 데이터를 범주형 데이터로 나누는 설명이 효과적일 수 있음
정규화
- 데이터가 가진 스케일이 심하게 차이나는 경우 상대적 특성이 반영된 데이터로 변환하는 것
일반 정규화
- 수치로 된 값들을 여러 개 사용할 때 각 수치의 범위가 다르면 이를 같은 범위로 변환하는 것
- 예) 연속형(이산형) 데이터 : 과목A는 10점 만점에서 8점, 과목B는 50점 만점에서 20점
- 일반 정규화 변환 : 과목A는 8/10=0.8점, 과목B는 20/50=0.4점, 평균은 0.6점
최소-최대 정규화(Min-Max normalization)
- 데이터를 정규화하는 가장 일반적인 방법
- 모든 특성(feature)에 대해 최소값 0, 최대값 1로 설정하고 값들을 0과 1 사이의 값으로 변환하는 것
- X에 대한 최소-최대 정규화 수식
- Min-Max Normalization = (X-Min) / (Max-Min)
- 예) X의 특성 : 최소값 20, 최대값 40
- 최소-최대 정규화 변환 : 중앙값 30, 0.5로 변환
- 단점으로는 이상치(outlier) 영향을 많이 받음
Z-점수(Z-Score) 정규화
- 이상치 문제를 피하는 데이터 정규화 전략
- Z-Score 정규화 수식 : Z = 원수치-평균 / 표준편차
- 예) 데이터의 값 평균으로 Z-점수 정규화
- 평균과 일치 : 0으로 정규화
- 평균보다 작음 : 음수로 정규화
- 평균보다 큼 : 양수로 정규화
- 단, 계산되는 음수와 양수의 크기는 데이터의 표준편차에 의해 결정
- 이상치는 잘 처리하지만 단점으로 정확히 동일한 척도로 정규화된 데이터를 생성하지 않음
로그변환(Log Transformation)
- 어떤 수치 값을 그대로 사용하지 않고 여기에 로그를 취한 값을 사용하는 것
- 로그를 취하면 정규 분포에 가깝게 분포하는 경우, 이런 분포를 로그 정규 분포를 가진다고 함
- 로그변환 분포 : X ~ log(X)
- 로그변환 분포를 사용한 전형적 데이터
- 국가별 수출액, 사람의 통증 정도 수치화, 개별주식의 가격이용 변동성 분석 등
- 데이터 분포의 형태가 우측으로 치우친 경우 정규분포화를 위한 로그변환 사용
제곱근변환(Square Root Transformation)
- 어떤 변수를 데이터 분석에 그대로 사용하지 않고 제곱근 사용
- 제곱근변환 분포 : X ~ √X
- 데이터 분포의 형태가 약간 우측으로 치우친 경우 사용
- 오히려 선형적인 특성을 가지게 되어 의미해석 쉬워짐
역수변환(Inverse Transformation)
- 어떤 변수를 데이터 분석에 그대로 사용하지 않고 역수 사용
- 역수변환 분포 : X ~ 1/X
- 데이터 분포의 형태가 극단적인 우측으로 치우친 경우 사용
- 오히려 선형적인 특성을 가지게 되어 의미해석이 쉬워짐
지수변환(Power Transformation)
- 어떤 변수를 데이터 분석에 그대로 사용하지 않고 지수 사용
- 지수변환 수식 : X ~ Xⁿ
- 데이터 분포의 형태가 좌측으로 치우친 경우 사용
- 오히려 선형적인 특성을 가지게 되어 의미해석이 쉬워짐
분포형태별 정규분포 변환
| 변수변환 전 분포 | 사용변수 변환식 | 변수변환 후 분포 |
| 좌로 치우침 | X³ | 정규분포화 |
| 좌로 약간 치우침 | X² | |
| 우로 약간 치우침 | √X | |
| 우로 치우침 | Log(X) | |
| 극단적 우로 치우침 | 1/X |
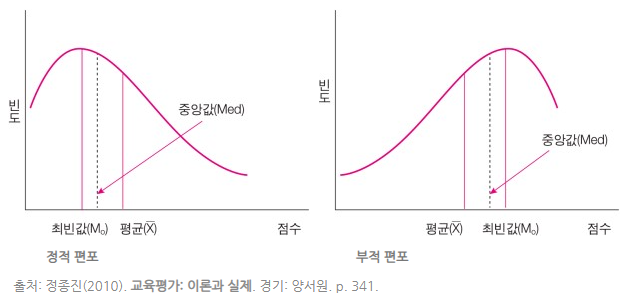
- 정적 편포(Positive Skew), 좌로 치우침
- 최빈값 < 중앙값 < 평균
- 정상분포(Symmetrical Distribution)
- 평균 = 중앙값 = 최빈값
- 부적 편포(Negative Skew), 우로 치우침
- 평균 < 중앙값 < 최빈값
* 최빈값(Mode), 중앙값(Median), 평균(Mean)
- 기본적인 단일집단 정규성 검정
- 샤피로테스트 또는 큐큐 플롯 이용해 확인 가능
- 결과에 따라 적당한 변수변환식을 사용하여 정규분포 형태로 변환
* 큐큐 플롯(Q-Q Plot) : 정규모집단 가정을 하는 방법 중 하나로 수집 데이터를 표준정규분포의 분위수와 비교하여 그리는 그래프
기타
- 데이터 축소 등
참고
반응형

