반응형
수학 수식을 우리가 볼 수 있는 수식처럼 표현해주는 라이브러리
포스팅에 기재되어 있는 기능들은 해당 라이브러리의 일부분입니다.
더 자세한 기능 및 계산, 수식 표현이 필요한 경우,
참고 부분에 기재되어 있는 공식 문서를 확인하시는 것을 권장드립니다.
(미분, 적분 부분 쪽은 이해가 잘 되지 않아 기본 공식 문서에서 있는 예제만 사용하였습니다. ㅠㅠ)
Sympy
- 기호 수학을 위한 파이썬 라이브러리
설치 및 사용 설정
설치
- 아나콘다 sympy 설치 명령어
conda install sympy
- 파이썬 sympy 설치 명령어
pip install sympy
# pip3 install sympy라이브러리 호출
import sympy
# from sympy import * : 표현하는 수학식 함수의 sympy.~ 부분을 생략 할 수 있음
# 예 : sympy.sqrt(8) -> sqrt(8)수식 출력 설정
- 사용자 환경에서 사용 할 수 있는 가장 최적의 형태의 문자로 출력
- 표현하기 어려운 수식 표현들을 보기 편하게 변경
- SymPy에서 출력 가능한 출력 형태
- str
- srepr
- ASCII pretty printer
- Unicode pretty printer
- LaTeX
- MathML
- Dot
# 수식을 사용자가 보기 좋은 형태로 출력
init_printing(use_unicode=True)수식 표현
제곱
제곱 : Pow
# 제곱 표현 : Pow(값, 제곱)
x = sympy.symbols("x")
sympy.Pow(x, 2)
제곱근(루트) : sqrt
# 제곱근(루트) 표현 : sqrt(숫자)
sympy.sqrt(8)
분수
분수 : Rational(분자, 분모)
# Rational : 유리수를 분수로 표현 (분자, 분모)
sympy.Rational(1,2)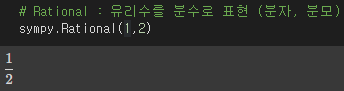
분수 : S('분자/분모/')
# S : 유리수를 분수로 표현 (분자, 분모)
sympy.S('1/2')
등식 : Eq
# 기호 등식 표현 : Eq(좌변, 우변)
x = sympy.symbols('x')
sympy.Eq(x + 1, 4)
미지수
미지수 기호 표현 : symbols
# 미지수 기호 표현 : symbols(기호 표현 문자)
x = sympy.symbols("x")
x
- 여러개의 미지수 기호 표현
# 여러개의 미지수 기호 표현
a, b, c, x, y, z = sympy.symbols("a, b, c, x, y, z")
a + b + c + x + y + z
미지수 기호의 제곱 : **
# 제곱 표현
x = sympy.symbols("x")
x ** 2
미지수 기호 값 변경 : subs
# 미지수 기호의 값 변경 : subs(원본값, 바꿀값)
x = sympy.symbols('x')
x.subs(x, 1)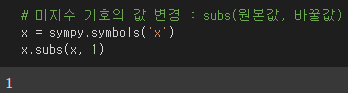
허수 : I
# 허수 표현, 대문자 i
I
원주율 : pi
# 원주율 표현
sympy.pi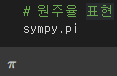
지수 함수 : exp
# 지수 함수 표현 : exp(x)
sympy.exp(x)
감마 함수 : gamma
# 감마 함수 표현 : gamma()
x = sympy.symbols("x")
sympy.gamma(x)
삼각함수
# 삼각 함수 표현 : 사인, 코사인 등 줄임말 그대로 입력
x = sympy.symbols('x')
sympy.sin(x) + sympy.asin(x) + sympy.sinh(x)
수식 단순화
일반적인 수식
simplify
# 표현한 수식을 더 간단한 수식으로 변환 : simplify(수식)
x = sympy.symbols("x")
sympy.simplify(sympy.gamma(x)/sympy.gamma(x - 2))
다항식 단순화
expand
- 다항식을 단항식 합의 정식 형식으로 변환
# 다항식을 단항합의 정식 형식으로 변환 : expand(수식)
x = sympy.symbols("x")
sympy.expand((x + 1)**2)
factor
- 다항식을 유리수에 대해 기약할 수 없는 인수로 인수분해
# 다항식을 유리수에 대해 기약할 수 없는 인수로 인수분해 : factor(수식)
x = sympy.symbols("x")
sympy.factor(x**3 - x**2 + x - 1)
factor_list
- 다항식을 인수분해한 수식으로 변환시 인자에 대한 구조화된 출력을 반환
# 다항식을 인수분해한 수식으로 변환시 인자에 대한 구조화된 출력을 반환 :factor_list(수식)
sympy.factor_list(x**2*z + 4*x*y*z + 4*y**2*z)
collect
- 다항식을 특정 기호에 대해 정리된 수식으로 변환
# 다항식을 특정 기호에 대해 정리된 수식으로 변환 : collect(수식, 기호)
x, y, z = sympy.symbols("x, y, z")
expr = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
collect(expr, x)
coeff
- 다항식의 특정 기호에 대한 계수를 반환
# 다항식의 특정 기호에 대한 계수를 반환 : ceoff(기호, 차수)
x, y, z = sympy.symbols("x, y, z")
expr = x**2*y + x*z + y*z
expr.coeff(x, 2)
유리식 단순화
cancel
- 유리식을 약분 형식으로 변환
# 유리식을 약분 형식으로 변환 : cancel(수식)
x = sympy.symbols('x')
sympy.cancel((x**2 + 2*x + 1)/(x**2 + x))
apart
- 유리식을 부분 분수로 분해한 형식으로 변환
# 유리식을 부분 분수로 분해한 형식으로 변환
x = sympy.symbols('x')
expr = (4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)
sympy.apart(4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)
수식 계산
미적분
미분
# 미분
sympy.diff(sympy.sin(x) * sympy.exp(x), x)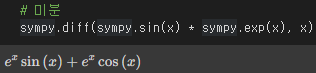
적분
# 적분
sympy.integrate ( sympy.exp(x)*sympy.sin(x) + sympy.exp(x)*sympy.cos(x), x)
참고
https://docs.sympy.org/latest/guides/assumptions.html
Assumptions - SymPy 1.11 documentation
Previous How-to Guides
docs.sympy.org
121 파이썬으로 방정식을 풀려면? ― sympy
sympy는 방정식 기호(symbol)를 사용하게 해주는 라이브러리이다. 마찬가지로 pip을 이용하여 라이브러리를 설치하자. ```no-highlight pip install …
wikidocs.net
http://allman84.blogspot.com/2018/10/sympy.html?m=1
파이썬 Sympy 기호수학 - 기초
파이썬 Sympy 기호수학 - 기초 $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad...
allman84.blogspot.com
반응형

