반응형
예시로 사용될 데이터프레임
- 회사 수익 예측하기
df = pd.read_csv('50_Startups.csv')
df.head()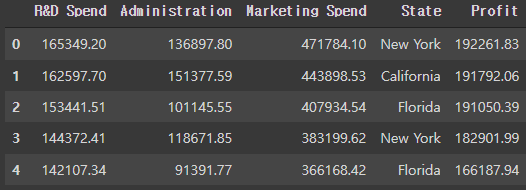
라이브러리 호출
# 데이터 가공
import numpy as np
import pandas as pd
# 카테고리컬 인코딩
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
# 피쳐 스케일링
from sklearn.preprocessing import MinMaxScaler
# 데이터셋 분리
from sklearn.model_selection import train_test_split
# 인공지능 모델링
import tensorflow as tf
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Dense학습 할 데이터와 예측 데이터 설정
# 학습 데이터 X
# X = Profit 컬럼 빼고 전부
X = df.iloc[ : ,0:-1]
# 예측 데이터 y
# y = Profit, 수익
y = df['Profit']문자열 데이터(State 컬럼) 정수로 치환

State 컬럼의 고유 값 확인
df['State'].unique()
>>> array(['New York', 'California', 'Florida'], dtype=object)
정수로 치환
# 카테고리컬 인코딩
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
ct = ColumnTransformer( [ ('encoder', OneHotEncoder(), [3] ) ], remainder='passthrough')
X = ct.fit_transform(X)
# 3개의 고유값에서 최적화를 위하여 한 개의 데이터 제거
X = X[ : , 1 : ]피쳐 스케일링
- y 데이터 형식 일관화 (2차원 배열로 변경)
- 인공지능은 2차원의 배열로 학습 할 수 있기 때문
# y 데이터는 Profit의 컬럼만 가지므로 시리즈 데이터를 2차원 배열로 변경 해야 함
y.shape
>>> (50, )
y = y.values.reshape(50, 1)
y.shape
>>> (50, 1)
- 서로 다른 범위의 정수의 데이터들을 일정 범위에 맞게 피쳐 스케일링 진행 (정규화)
- m_sc_X : 학습 데이터 X를 정규화하는 스케일러
- m_sc_y : 예측 데이터 y를 정규화하는 스케일러
- X_scaled : 정규화 된 X의 값을 가지는 변수
- y_scaled : 정규화 된 y의 값을 가지는 변수
# 피쳐 스케일링
from sklearn.preprocessing import MinMaxScaler
m_sc_X = MinMaxScaler()
m_sc_y = MinMaxScaler()
X_scaled = m_sc_X.fit_transform(X)
y_scaled = m_sc_y.fit_transform(y)인공지능 학습을 위한 학습용과 검증용 데이터 분리
# 데이터셋 분리, 기본 값 테스트 사이즈 25%
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, random_state = 3)인공신경망 모델링
인공지능 모델 생성
model = Sequential()
레이어 설정
- 유닛과 활성함수는 원하는대로 설정
- 첫번째 input layer는 반드시 입력층의 형태를 지정
- 마지막 output layer는 분류 문제의 모델이 아니기 때문에 sigmiod 사용하지 않음
model.add( Dense(units=5, activation='relu', input_shape=( 5 , )) )
model.add( Dense(units=15, activation='relu') )
model.add( Dense(units=10, activation='relu') )
model.add( Dense(units=1, activation='linear') )
컴파일 설정
- 옵티마이저는 잘 모르겠으면 보편적으로 adam을 쓰는 것이 좋음 (무조건은 아닙니다!)
model.compile(loss='mse', optimizer='adam')학습 및 측정
- epoch_history : 임의의 변수, 학습 내용을 저장 (오차(손실) 확인용도)
- epochs : 모델의 전체 데이터 셋에서 학습 횟수
- batch_size : 샘플의 갯수대로 학습 한 후 가중치 갱신
# 학습 결과 변수에 저장
# 200번 학습, 10번 단위로 가중치 갱신
epoch_history = model.fit(X_train, y_train, epochs=200, batch_size=10)예측
- 학습한 모델을 이용하여 결과값 예측 (predict)
# 결과값 예측
y_pred = model.predict(X_test)
# 결과값 확인
y_pred
>>>
array([[0.6389722 ],
[0.36450982],
[0.7447857 ],
[0.08885911],
[0.52901554],
[0.53316796],
[0.65977514],
[0.38273808],
[0.33775404],
[0.68797165],
[0.3954041 ],
[0.5779902 ],
[0.33800676]], dtype=float32)
# 실제값 확인
y_test
>>>
array([[0.71462897],
[0.37348913],
[0.7606613 ],
[0.15698988],
[0.46627976],
[0.49893437],
[0.67364377],
[0.11821128],
[0.28294041],
[0.79649041],
[0.42812595],
[0.52963376],
[0.42385155]])실제값과 예측값 비교
- 분류 문제의 모델이 아니기 때문에 차트로 보는게 가시성이 가장 좋음
import matplotlib.pyplot as plt
plt.plot(y_test, c='r') # 실제값은 빨간선
plt.plot(y_pred, c='b') # 예측값은 파란선
plt.show()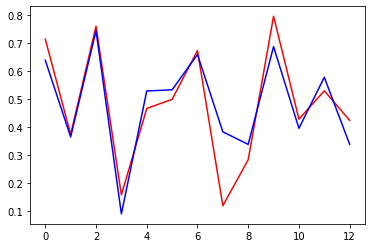
인공신경망 모델의 오차(손실) 확인
- 최종 값이 낮을수록 모델의 성능이 향상, 즉 정확도가 높아짐
plt.plot(epoch_history.history['loss'])
plt.show()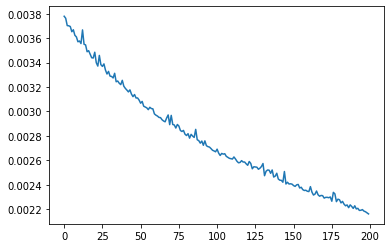
반응형

