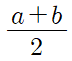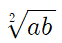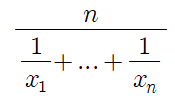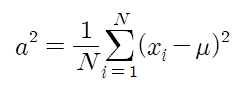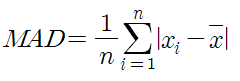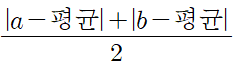기초통계량
- 자료를 수집하여 요약/정리하는 기초통계 또는 기술통계
- 자료의 특성을 정량적인 수치에 의해서 나타내는 방법
- 자료의 특성을 수치적 결과로 표현
- 중심화 경향(Central Tendency)
- 퍼짐 정도(산포도/분산도)
- 자료의 분포 형태(Shape of distribution) 등
중심화 경향 기초통계량
산술평균(Arithmetic Mean)
- 모든 자료들을 합한 후 전체 자료수로 나누어 계산하는 일반적인 평균을 의미
- 모평균(Population Mean)모집단 전체 자료의 산술평균
- 표본평균(Sample Mean) : 모집단의 부분집합인 추출된 표본 전체의 산술평균
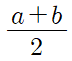
기하평균(Geometric Mean)
- N개의 자료에 대해 관측치를 곱한 후 n 제곱근으로 표현하는 것
- 즉, 산술평균은 합의 평균 / 기하평균은 곱의 평균
- 다기간의 수익률에 대한 평균 수익률, 평균물가상승률 등을 구할 때 사용
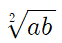
- 예시) 첫 번째 해에 2%, 두번째 해에는 8%의 수익이 증가했다. 연평균 증가율은?
조화평균(Harmonic Mean)
- 각 요소의 역수의 산술평균을 구한 후 다시 역수를 취하는 형태로 표현하는 것
- 변화율, 주로 속도와 관련된 데이터 등의 평균을 구할 때 사용
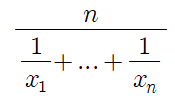
- 예시) 갈 때 10m/s, 올 때 20m/s로 주행하였을 때의 평균 속력은?
자료에 대한 부등식 관계
- 각 자료가 동일한 경우 : 조화평균 = 산술평균 = 기하평균
- 각 자료가 서로 다를 경우 : 조화평균 <= 기하평균 <= 산술평균
중앙값(Mean)
- 자료를 크기 순으로 나열할 때 가운데에 위치한 값
- 자료의 수를 n이라 할 경우 중앙값 정의
- 홀수 n : (n+1)/2번째 자료값
- 짝수 n : n/2번째와 n/2+1번째 자료의 평균
- 예시) 1, 40, 100 세 수가 있을 때 중앙 값은?
- n이 홀수인 3(세 수)
- 3+1 / 2 = 2, 즉 두번째 값(40)이 중앙값
최빈값(Mode)
- 가장 노출 빈도가 높은 자료
- 질적자료나 양적자료 모두에 사용
- 예시) 1, 2, 2, 3, 3, 3 의 값이 주어질 경우의 최빈값은?
- 3이 가장 많이 관측되는 수 이므로 최빈값은 3
분위수(Quantile)
- 자료의 위치를 표현하는 수치
- 자료를 크기순서대로 배열한 후 자료를 분할하는 역할을 하는 위치의 수치를 계산한 것
- 자료를 몇 등분을 하느냐에 따라 분위수는 달라짐
- 예시) 자료를 사분위수로 나누면?
- Q1: 제1사분위수, 0~25%지점
- Q2: 제2사분위수, 25~50%지점
- Q3: 제3사분위수, 50~75%지점
- Q4: 제4사분위수, 75~100%지점
산포도(분산도, Degree Dispersion)
- 자료의 퍼짐 정도를 나타내는 기초 통계량
- 중심 위치의 측도만으로 자료의 분포에 대한 충분한 정보를 얻을 수 없음
- 중심 경향도 수치에서 자료가 얼마나 떨어져 있는지를 측정하는 척도 필요
분산(Variance)
- 평균을 중심으로 밀집되거나 퍼짐 정도를 나타내는 척도
- 개개의 자료값과 평균과의 편차의 제곱을 이용하여 표현
- 분산의 특성
- 개개의 자료값에 대한 정보 반영
- 수리적으로 다루기 쉬움
- 특이점에 매우 큰 영향을 받음
- 분산이 클수록 각 자료값이 평균으로부터 넓게 흩어진 형태를 가짐
- 미지의 모분산을 추론할 때 많이 사용
- 단점 : 얻은 수치 해석의 어려움
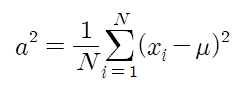<모분산 수식>
표준편차
- 분산의 제곱근으로 표현
- 분산의 단점을 보완하기 위해 제곱근을 취한 척도
<모표준편차 수식>
모분산과 모표준편차의 예시
- 예시) 여러 자산에 투자수익률이 20%와 30%일 경우, 모분산과 표준편차는?
- 평균 : 20+30/2 = 25%
- 모분산 : (20-25)^2 + 30-25)^2 / 2 = 25
- 모표준편차 : 루트25 = 5
범위
- 데이터 간의 최댓값과 최솟값의 차이를 나타낸 것
- 동일한 범위를 갖더라도 자료의 분포모양은 다를 수 있음에 유의
평균 절대 편차(평균 편차, 절대 편차, MAD: Mean Absolute Deviation)
- 각 자료값과 표본평균과의 편차의 절댓값에 대한 산술평균을 의미
- 관측값에서 평균을 빼고, 그 차이값에 절댓값을 취한 값들을 모두 더하여 전체 데이터 개수로 나눠 준 것
- 평균 절대 편차의 특성
- 개개의 자료값에 대한 정보 반영
- 이상치에 대한 영향을 범위보다 적게 받음
- 절댓값 사용으로 수리적으로 다루기 부적절함
- 편차는 특정 대푯값으로 떨어진 거리를 의미
- 절대 편차의 최소값을 갖는 자료값은 평균이 아닌 중앙값
- 절대 편차는 미분 불가능점이 존재
- 평균 절대 편차가 클수록 자료는 폭넓게 분포
- 중앙값 절대 편차를 사용할 때 유용
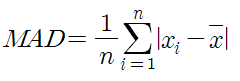
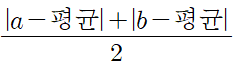
- 예시) 여러 자산에 투자수익률이 20%와 30%일 경우, 평균 절대 편차는?
- 평균 : 20+30/2 = 25%
- 평균 절대 편차
- 20-5| + |30-5| / 2
- > 5 + 5 / 2 = 5
사분위범위(Inter Quartile Range)
- 자료의 50% 범위 내에 포함되는 자료
- 자료를 크기 순으로 배열
- 자료의 1/4에 해당하는 1사분위수(Q1)를 구함
- 자료의 3/4에 해당하는 3사분위수(Q3)를 구함
- 사분위범위는 Q3-Q1로 정의
- 주로 이상치 판단 시 사용
- 결정된 최대값보다 크거나 최소값보다 작은 값을 이상치로 간주
- 예시) 다음 수의 사분위를 구하고 사분위수의 범위는? { 1, 3, 3, 3, 4, 4, 4, 6, 6 }
- 중앙값
- 총 갯수가 9개(홀수)
- 5번째에 위치한 값이 중앙값(4)
- 중앙값을 기준으로 왼쪽의 값들의 중앙값
- 1, 3, 3, 3, 4(중앙값) 총 갯수가 4개(짝수)
- 2번째와 3번째의 값의 평균
- 즉, Q1(제1사분위)는 3
- 중앙값을 기준으로 오른쪽 값들의 중앙값
- 4(중앙값), 4, 4, 6, 6 총 갯수가 4개(짝수)
- 2번째와 3번째의 값의 평균
- 즉, Q3(제3사분위)는 5
- 사분위수의 범위
- Q3 - Q1
- 5 - 3 = 2
- 사분위수의 범위 : 2
변동계수(CV: Coefficent of Variance)
- 평균을 중심으로 한 상대적인 산포의 척도를 나타내는 수치
- 두 자료집단에 대한 산포의 척도를 비교할 때 많이 사용
- 측정 단위가 동일하지만 평균이 큰 차이를 보이는 두 자료집단일 경우
- 측정 단위가 서로 다른 두 자료집단일 경우
- 예시) A의 평균 수익률은 30%, 표준편차는 4% / B의 평균 수익률은 15%, 표준편차는 3%일 때 A,B의 변동계수는?
- A의 변동계수
- B의 변동계수
- B의 수익 변동이 더 크다고 판단
자료의 분포형태(Shape of Distribution)
왜도(Skewness)
- 분포가 어느 한쪽으로 치우친 정도를 나타내는 통계적 척도
<왜도(편포도 혹은 비대칭도) 정규분포의 예시>
- 정적 편포(Positive Skew), 좌로 치우침
- 정상분포(Symmetrical Distribution)
- 부적 편포(Negative Skew), 우로 치우침
첨도(Kurtosis)
- 분포의 표족한 정도를 나타내는 통계적 척도
- 평평한 분포
- 정규분포
- 뾰족한 분포
참고
